Approach to Solve Complex Advanced Calculus Assignments

Advanced Calculus is a challenging subject that explores the foundational concepts of mathematical analysis, and solving assignments in this field can often feel overwhelming. The subject covers a wide range of topics, including the field of complex numbers, topology, sequences and series, continuity, differentiation, and integration. Each of these topics requires a solid understanding of underlying principles and a strategic approach to problem-solving.
To tackle Advanced Calculus assignments effectively, it's essential to break down each problem step by step. For instance, understanding how to apply the Heine-Borel theorem for compact sets, or using Taylor's theorem for differentiating functions, can be crucial. Similarly, knowing how to work with Cauchy sequences and apply the Ratio Test for series convergence can simplify complex problems.
If you're finding it challenging to navigate through the intricacies of Advanced Calculus, it might be helpful to seek expert guidance. A professional can help you solve your advanced calculus assignment, ensuring you not only get the right answers but also understand the core concepts deeply. Whether it’s applying the Intermediate Value Theorem or tackling integration problems, having the right support can make all the difference in mastering these advanced topics and succeeding in your assignments.

The Field of Complex Numbers and Real Number Systems
In Advanced Calculus, understanding the structure of real and complex numbers is foundational. The real number system, denoted R, is an ordered field, meaning it is equipped with both addition and multiplication operations. The extended real number system R‾, which adds +∞ and −∞, plays a key role when dealing with limits and improper integrals.
When dealing with complex numbers, denoted C, you should be comfortable with complex functions, limits, and their applications in solving real-world problems. The focus here is on understanding the topology of C and its connection to real numbers. A common assignment may ask for proving that a sequence of complex numbers converges, using limits such as:
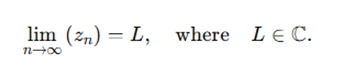
Topology and Metric Spaces
Basic topology is crucial when working with spaces like Rn. In assignments on this topic, focus on concepts like finite, countable, and uncountable sets. For example, you may be tasked with proving whether a given set is uncountable or showing the compactness of certain metric spaces. The Heine-Borel theorem, which characterizes compact subsets of Rn, states that:
A set in Rn is compact if and only if it is closed and bounded.
Understanding compactness and connectedness is essential for completing problems related to sequences and their limits. Pay close attention to how compact sets behave under continuous functions. In practice, you'll likely work with sequences and series whose convergence depends on these properties.
Sequences and Series: Convergence Criteria
Convergence is a central concept in Advanced Calculus. Problems related to sequences and series often ask you to prove whether a sequence converges or to find its limit. Cauchy sequences are especially important because they help you establish the completeness of Rn. If a sequence{a_n}{an} is a Cauchy sequence, then it will converge in a complete metric space like Rn.
In an assignment, you might encounter a problem that requires determining the limit of a series, such as:
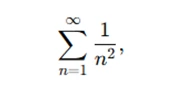
and proving whether it converges or diverges. Convergence criteria like the Ratio Test or the Root Test are essential for such tasks. Understanding these tests will make it easier to solve related problems.
Continuity: Limits and Intermediate Value Theorem
When solving problems on continuity, the key is to establish whether a function is continuous at a given point or within a region. For example, if you have a function f:U→Rm, where U⊆Rn, your task is often to prove that f is continuous using the definition of continuity:
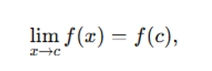
where c ∈ U. The Intermediate Value Theorem is often invoked in these problems, which states that if a function is continuous on a closed interval, then it attains every value between its minimum and maximum.
Differentiation of Functions of One Variable
Differentiation is a fundamental concept in calculus, and in assignments, you'll need to apply various theorems to solve differentiation problems. The Mean Value Theorem (MVT) is often used to prove that a function behaves in a specific way on an interval. If f is continuous on [a,b] and differentiable on (a,b), the MVT asserts that there exists some c∈(a,b) such that:
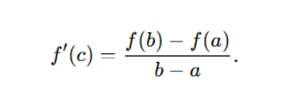
Another essential tool is Taylor’s Theorem, which provides an approximation of functions as polynomials. For example, the Taylor series of a function f(x) around aaa is given by:
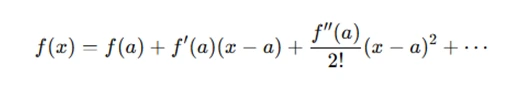
Integration of Functions of One Variable
When dealing with integration, the Riemann-Stieltjes integral is often introduced in Advanced Calculus assignments. This integral generalizes the Riemann integral by considering integration with respect to a function g, instead of just x:
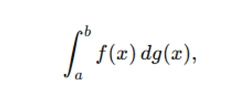
where g(x) is a function that may have jumps or other peculiarities. The existence of the Riemann-Stieltjes integral requires careful attention to the properties of f and g.
Sequences and Series of Functions
A sequence of functions is a powerful tool in analysis. If fn(x) is a sequence of functions, understanding uniform convergence is crucial. The Arzela-Ascoli theorem helps identify when a sequence of functions converges uniformly, which is important for interchanging the order of limit and integration or differentiation. The Stone-Weierstrass theorem is also fundamental in proving the approximation of continuous functions by polynomials.
Conclusion
Approaching assignments in Advanced Calculus requires a deep understanding of concepts and a systematic method of solving problems. Start by understanding the underlying theory behind complex numbers, topology, sequences, and series. Then, tackle problems step by step, applying the appropriate theorems such as the Heine-Borel theorem or the Intermediate Value Theorem to find solutions. By maintaining clarity on key concepts like continuity, differentiation, and integration, you can successfully complete your math assignment and gain a deeper appreciation of this advanced field of mathematics.