Banach and Hilbert Spaces: Key Concepts for Functional Analysis Assignments

Dr. James Thompson

United Kingdom

Functional Analysis

Dr. James Thompson, with over 10 years of experience in functional analysis, holds a Ph.D. in Mathematics from the University of Aberdeen, UK.

Hire Me To Do Your Functional Analysis Assignment

What Are Banach Spaces?

A Banach space is a vector space equipped with a norm, where the space is complete with respect to that norm. This means that every Cauchy sequence in the space converges to an element within the space. The completeness property is key to ensuring that limits of sequences, which may arise in analysis, always remain within the space. Banach spaces are fundamental in functional analysis because they provide a framework for studying linear operators, integration, and differentiation. They are commonly used in problems involving convergence, approximation, and the behavior of operators, making them an essential tool for many areas of mathematics, particularly in analyzing infinite-dimensional spaces where traditional methods may not apply.

Definition of a Banach Space

A normed vector space XXX is a Banach space if it satisfies the following conditions:

• Norm: There exists a function ∥⋅∥:X→R, called a norm, such that for any vectors x,y∈X, the following properties hold:
• ∥x∥≥0 and ∥x∥=0  ⟺  x=0
• ∥x+y∥≤∥x∥+∥y∥ (Triangle inequality)
• ∥αx∥=∣α∣∥x∥, where α is a scalar.
• Completeness: A space is complete if every Cauchy sequence (xn) in X has a limit in X. A Cauchy sequence is one where the elements of the sequence become arbitrarily close to each other as the sequence progresses.

Examples of Banach Spaces

1. ℓp Spaces: The space of sequences { xn} such that the series ∑∣xn∣p converges is a Banach space when equipped with the p-norm:

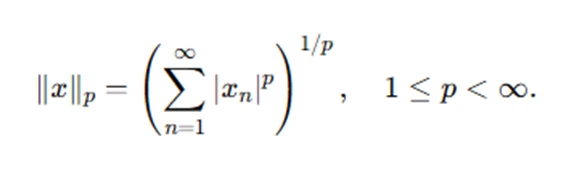
The space ℓ∞ (the space of bounded sequences) is also a Banach space.

2. Continuous Functions Space: The space C([a,b]) of continuous real-valued functions on a closed interval [a,b] with the supremum norm:

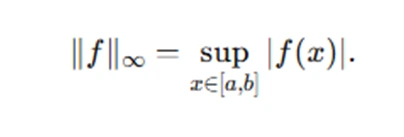
This is also a Banach space.

What Are Hilbert Spaces?

A Hilbert space is a specific type of Banach space where the norm is derived from an inner product, giving it a richer geometric structure. This inner product enables key concepts like orthogonality, projections, and Fourier series, which are central in functional analysis. In a Hilbert space, you can define orthogonal vectors, allowing for the decomposition of functions or signals into orthogonal components, which is particularly useful in signal processing and quantum mechanics. The inner product in Hilbert spaces also facilitates the study of operator theory, enabling the analysis of linear operators, their eigenvalues, and spectral properties. This structure makes Hilbert spaces ideal for applications where understanding the geometric and analytical behavior of functions is crucial. In quantum mechanics, Hilbert spaces provide the mathematical framework for describing quantum states, while in signal processing, they help in understanding the decomposition and reconstruction of signals, such as through Fourier transforms.

Definition of a Hilbert Space

A Hilbert space H is a complete inner product space. This means it satisfies the following:

• Inner Product: There exists a function ⟨⋅,⋅⟩:H×H →C (or R) satisfying:
• ⟨x,y⟩=⟨y,x⟩ (conjugate symmetry)
• ⟨x,x⟩≥0 and x, x =0  ⟺  x=0 (positive definiteness)
• ⟨x+y,z⟩=⟨x,z⟩+⟨y,z⟩ (linearity in the first component)
• ⟨αx,y⟩=α⟨x,y⟩ for any scalar α\alphaα.
• Induced Norm: The norm in a Hilbert space is induced by the inner product:



• Completeness: A Hilbert space is complete in the sense that every Cauchy sequence of vectors in the space converges to a limit that lies within the space.

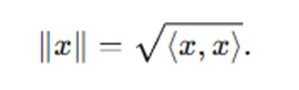
Examples of Hilbert Spaces

1. L2LSpace: The space of square-integrable functions on an interval [a,b], denoted L2([a,b]), is a Hilbert space with the inner product:

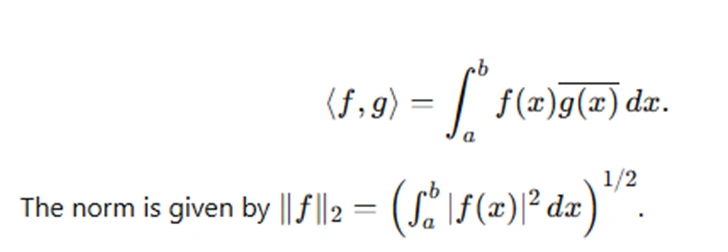
2. ℓ2 Space: The space of square-summable sequences {xn}, where ∑n=1∞∣xn∣2<∞ is a Hilbert space with the inner product:

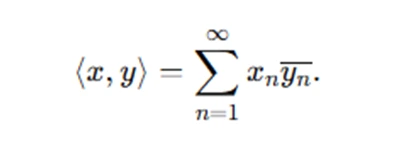
Key Differences Between Banach and Hilbert Spaces

While both Banach and Hilbert spaces are vector spaces with a norm, the main distinction lies in the type of structure they possess.

• Norm vs. Inner Product
• Banach Space: Defined by a norm (no inner product is necessary).
• Hilbert Space: Defined by an inner product, which induces a norm.
• Geometric Structure
• Banach Space: Lacks the rich geometric structure that comes with inner products, meaning concepts like orthogonality and projections are not as naturally defined.
• Hilbert Space: Equipped with a geometric structure due to the inner product, making concepts like orthogonality, projection, and Fourier series possible.
• Examples
• Banach Space: ℓp spaces, continuous functions spaces.
• Hilbert Space: ℓ2, L2 spaces.

Solving Functional Analysis Assignments Using Banach and Hilbert Spaces

Understanding Banach and Hilbert spaces is essential for tackling functional analysis assignments. Banach spaces, with their normed structure and completeness, provide a solid foundation for analyzing convergence and working with operators. Hilbert spaces, with their inner product structure, offer a rich geometric framework that allows for concepts like orthogonality, projection, and Fourier analysis. Mastering these spaces helps in solving problems related to operator theory, spectral analysis, and convergence, particularly in spaces like ℓ2 and 𝐿2. Gaining a solid grasp of these concepts will improve your ability to solve complex functional analysis problems effectively. Below are key strategies for using these spaces in various types of problems.

1. Working with Cauchy Sequences and Convergence

When given a problem involving Cauchy sequences or convergence in a Banach or Hilbert space, remember that completeness is a key property. For example, if you need to prove that a sequence converges, check whether it forms a Cauchy sequence and if the space is complete.

For Hilbert spaces, you can also leverage the Pythagorean theorem and projection theorems to simplify convergence problems, particularly in spaces like ℓ2 or L2.

2. Operator Theory and Functional Analysis

Banach and Hilbert spaces are commonly used in problems involving operators. For instance, you may be asked to find the spectrum of an operator or solve for eigenvalues and eigenvectors.

• In Banach spaces, you can use bounded linear operators and the Banach-Steinhaus theorem (also known as the uniform boundedness principle) to work with operators and their properties.
• In Hilbert spaces, you often deal with self-adjoint operators, orthonormal bases, and Fourier series. The Riesz representation theorem is particularly helpful in proving the existence of certain functionals and operators.

3. Fourier Analysis

Fourier analysis heavily relies on the properties of Hilbert spaces, especially in spaces like L2 and ℓ2. In these spaces, you can decompose functions or sequences into a sum of orthogonal components (Fourier series) and analyze them in terms of their spectral properties.

For functional analysis assignments involving Fourier transforms, remember that the Hilbert space structure allows for the application of orthogonal projections, which makes decomposing functions or signals into simpler components more manageable.

4. Proving Completeness

A frequent problem in functional analysis is proving that a given space is complete. If you're working in a Banach space, check whether Cauchy sequences converge in that space. For Hilbert spaces, the Bessel inequality and Parseval's theorem can help in proving completeness, especially when dealing with Fourier series or orthogonal expansions.

Conclusion

Banach and Hilbert spaces are essential concepts in functional analysis, offering a solid foundation for understanding operator theory, convergence, and Fourier analysis. Banach spaces are normed vector spaces that are complete, meaning every Cauchy sequence converges within the space. Hilbert spaces, a special case of Banach spaces, are inner product spaces with a rich geometric structure, enabling concepts like orthogonality and projections. Understanding their differences, such as the role of inner products in Hilbert spaces, is key to tackling functional analysis assignments. These spaces provide powerful tools for solving problems involving convergence, operators, and spectral analysis. To excel in assignments, practice applying these concepts through problems on Cauchy sequences, operator theory, and Fourier analysis. Seeking assistance with math assignment can help you grasp these challenging topics. Mastering Banach and Hilbert spaces will deepen your understanding of functional analysis and equip you to handle complex mathematical problems with confidence.