Approaching Complex Combinatorial Optimization Assignment Problems

Combinatorial optimization focuses on finding the best solution from a finite set of possibilities, typically under specific constraints. It involves techniques like greedy algorithms, matching theory, and polyhedral theory to address problems that arise in various fields such as computer science, operations research, and network design. Greedy algorithms, for example, are used to solve problems like minimum spanning trees and shortest paths by iteratively selecting the best option at each step. Matching theory is employed in problems such as bipartite matching and nonbipartite matching, while polyhedral theory helps in understanding the structure of feasible solutions in optimization problems. These methods are essential for solving a range of combinatorial problems and are frequently encountered in assignments, where students apply these techniques to find optimal or near-optimal solutions. Mastering combinatorial optimization helps improve problem-solving skills and prepares students for real-world challenges in optimization. In this blog, we will break down how to solve your optimization assignment specifically related to the following combinatorial optimization techniques: greedy algorithms, shortest path algorithms, and max-flow/min-cut, offering a detailed explanation for each.
1. Greedy Algorithms for Spanning Trees and Matroids

Greedy algorithms are a foundational tool in combinatorial optimization, often applied in problems like finding the minimum spanning tree of a graph or solving matroid optimization problems. The principle behind greedy algorithms is simple: choose the locally optimal solution at each step, with the hope that these local choices will lead to a global optimum.
Prim’s Spanning Tree Algorithm is one such example, which works by starting from an arbitrary node and growing the spanning tree by always selecting the minimum weight edge that connects a node in the tree to a node outside of it. The algorithm guarantees the optimal solution for the minimum spanning tree problem.
To approach this problem, consider the following equation for the weight of the spanning tree:
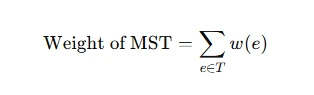
where T is the set of edges in the spanning tree, and w(e) is the weight of an edge e. Prim's algorithm keeps adding the smallest edge e=(u,v) where u is in the tree and v is not, minimizing the total weight.
2. Shortest Path Algorithms
When solving shortest path problems in assignments involving graphs with weighted edges, algorithms like Dijkstra’s Algorithm are commonly used. The core idea behind Dijkstra’s algorithm is to maintain a set of nodes with known shortest distances from the source node. Initially, the distance to the source node is set to zero, and the distances to all other nodes are set to infinity. The algorithm works by selecting the node with the smallest known distance, marking it as visited, and updating the distances to its neighboring nodes. This process continues until the shortest path to all nodes is determined. Each time a node is visited, the algorithm updates the shortest distance to its neighboring nodes, ensuring that the shortest paths are progressively found. Dijkstra’s algorithm is efficient and widely used for graph-related problems, especially when dealing with weighted edges in math assignments.
The equation that defines the shortest path from the source node s to a node v is:
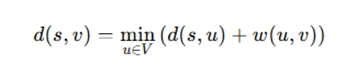
where d(s,v) represents the shortest path from the source s to node v, and w(u,v) is the weight of the edge between nodes u and v.
3. Max-flow/Min-cut and Edmonds-Karp Algorithm
The Max-Flow/Min-Cut Theorem states that in a flow network, the maximum flow is equal to the capacity of the minimum cut that separates the source and sink. This means that the maximum flow that can be pushed through the network is constrained by the smallest capacity cut in the network. The Edmonds-Karp Algorithm, a specific implementation of the Ford-Fulkerson method, provides an efficient way to compute this maximum flow. It works by repeatedly finding augmenting paths in the residual graph and adjusting the flow accordingly. Each augmenting path increases the total flow, and the process continues until no more augmenting paths can be found. The algorithm terminates when the flow reaches its maximum, and the residual graph indicates the corresponding minimum cut. This approach helps solve complex flow network problems, making it crucial for applications such as network optimization and resource allocation.
To solve an assignment involving this theorem, use the following equation to compute the flow:
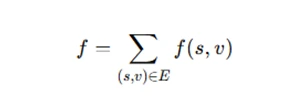
where f(s,v) represents the flow from node s to node v, and E is the set of edges in the graph.
The min-cut is defined as:
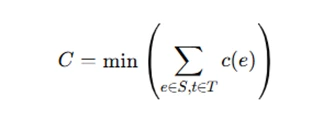
where S and T represent the partitions of the graph that separate the source and sink, and c(e) is the capacity of edge e.
Formulating Integer Programs and Branch and Bound
Integer programming problems are frequently encountered in combinatorial optimization when variables are required to take integer values. To solve these problems, one effective approach is the branch and bound method. This technique involves systematically exploring the solution space by dividing the problem into subproblems (branching) and eliminating subproblems that cannot lead to optimal solutions (bounding). At each branch, the algorithm evaluates the objective function and the constraints, progressively narrowing down the search space. If a subproblem’s solution is not feasible or cannot outperform the best solution found so far, it is pruned from the search. This process continues until the optimal solution is found. Branch and bound is particularly useful for solving problems like scheduling, network design, and allocation, where decision variables are required to be integers. It provides a structured way to address complex optimization challenges effectively.
For example, in a maximization integer program:
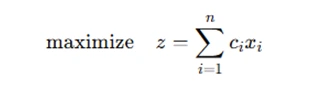
subject to:
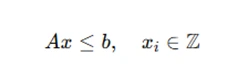
where xi are integer variables, ci are coefficients, and A and b represent the constraints.
Conclusion
In conclusion, solving combinatorial optimization problems requires a systematic approach, combining theory with practical algorithms. Whether you're tackling greedy algorithms, shortest path problems, or max-flow/min-cut theory, each problem can be broken down into manageable steps using the appropriate mathematical methods. For example, Prim's algorithm helps efficiently find minimum spanning trees, while Dijkstra's algorithm ensures the shortest path between nodes. In more complex cases, integer programming and branch-and-bound techniques offer solutions for optimization problems with integer constraints. These methods not only play a key role in academic assignments but also in real-world applications, making combinatorial optimization a vital area of study. As you complete your math assignment or any combinatorial problem, focus on translating each challenge into mathematical equations and systematically applying the most suitable algorithm. By mastering these techniques, you can efficiently navigate through complex optimization problems and achieve optimal solutions.