Understanding Core Concepts to Solve Complex Analysis Assignments

Complex Analysis is a subject that offers both depth and elegance, making it a fascinating yet challenging field of study. Solving assignments in this domain requires a clear understanding of core principles, a methodical approach, and the ability to apply theoretical concepts to practical problems. Each topic in Complex Analysis, from analytic functions to singularities, has its own nuances and intricacies.
When tackling assignments, it’s important to break down the problem into manageable parts. For instance, verifying the analyticity of a function might involve checking the Cauchy-Riemann equations or using power series expansions. Similarly, evaluating integrals often relies on tools like the Cauchy integral formula or residue theorem. These methods not only simplify problems but also reveal the underlying beauty of complex functions.
Approaching each topic systematically helps you connect the dots between theory and application. With practice and careful analysis, you can build the confidence to solve your complex analysis assignment and master the subject’s fundamental concepts.

1. Analytic Functions and Equivalent Conditions
A function f(z) is analytic if it satisfies the limit of the difference quotient:
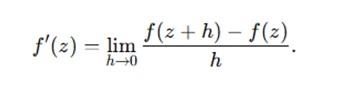
This definition is fundamental to verifying the differentiability of functions in complex analysis. In assignments, you'll often be tasked with proving a function's analyticity using the Cauchy-Riemann (CR) equations:
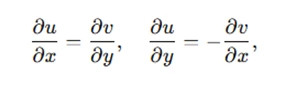
where f(z)=u(x,y)+iv(x,y) To approach such problems, break down the function into its real (u) and imaginary (v) parts, compute partial derivatives, and check if they satisfy the CR equations.
Another powerful tool is Morera’s theorem, which states that if f(z) is continuous on a domain D and satisfies ∫γf(z) dz=0 for every closed curve γ in D, then f(z) is analytic in D. In your assignments, you might need to construct specific closed curves or verify this property using symmetry arguments.
Lastly, power series expansions provide a straightforward way to analyze functions. Assignments may require expressing f(z) as ∑n=0∞ an (z−z0)n and determining the radius of convergence.
2. Cauchy’s Theorem and Its Consequences
Cauchy’s theorem is a cornerstone of Complex Analysis, stating that if f(z) is analytic on and within a closed contour γ, then ∫γf(z) dz=0. In assignments, proving this often involves confirming analyticity and demonstrating that the contour lies within the function’s domain.
The Cauchy integral formula takes this a step further, allowing you to evaluate functions inside a contour:
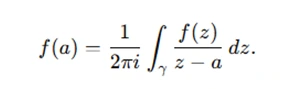
Assignments frequently leverage this formula to compute specific function values or derivatives. For example, if γ\gammaγ is the unit circle, you can calculate f(0) or f′(0) by integrating f(z)/(zn).
Consequences of Cauchy’s theorem, like Liouville’s theorem, often appear in proofs. For instance, in a problem asking whether a bounded entire function can be non-constant, use Liouville's theorem to conclude it must be constant. Similarly, the open mapping theorem is invaluable for showing how analytic functions map open sets to open sets.
Another powerful result is the residue theorem, which simplifies complex integrals by summing residues of singularities within the contour. In assignments, you might need to calculate residues at poles using:
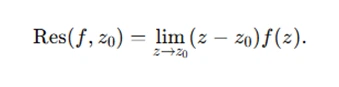
3. Elementary Functions and Their Mapping Properties
Elementary functions like ez, sin z, and rational functions play a significant role in Complex Analysis. Assignments often involve understanding their definitions, mapping properties, and special behaviors.
Linear fractional transformations (LFTs), defined as w= az+b/cz+d are a common focus. These transformations map circles and lines in the complex plane to other circles and lines. To solve problems on LFTs, use fixed points or compute images of critical points like 0, 1, and ∞.
For instance, an assignment might ask you to show how w= 1/ z maps the unit circle ∣z∣ =1 to itself, with an inversion. Understanding such mappings helps unravel the behavior of more complex functions.
4. Power Series and Singularities
Power series are a versatile tool for analyzing complex functions. Assignments often require finding the region of convergence, which is determined by the radius R:
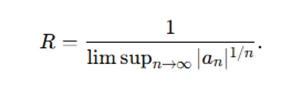
Boundary behavior can be explored by testing specific points on ∣z−z0∣=R. Singularities form another crucial topic. Classify them as:
- Removable singularities: If limz→z0 f(z) exists, the singularity is removable.
- Poles: A singularity is a pole of order n if (z−z0)n f(z) is analytic and non-zero at z0z_0z0.
- Essential singularities: Identified using the Casorati-Weierstrass theorem or Picard’s theorem, these exhibit unpredictable behavior.
Assignments may also ask for contour integrals around singular points or the residue at each singularity to simplify complex expressions.
5. Sequences and Normal Families
In assignments on sequences of functions, the focus is often on proving uniform convergence. Use definitions and inequalities to show that:
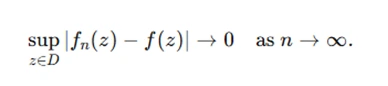
Normal families, where every sequence has a subsequence converging uniformly, often appear in questions involving Montel’s theorem. You might be required to show that a family of functions is normal by proving boundedness or equicontinuity.
Conclusion
Complex Analysis is a subject that beautifully blends theoretical rigor with practical problem-solving. Assignments in this area demand a structured approach to tackle intricate topics like analytic functions, Cauchy’s theorems, power series, singularities, and mapping properties. By understanding the foundational concepts, applying relevant theorems, and using precise calculations, you can solve even the most challenging problems effectively.
The key lies in breaking down each problem, focusing on the specifics, and ensuring logical consistency in your solutions. Regular practice and revisiting essential theorems, such as Cauchy’s integral formula or the residue theorem, not only help to solve your math assignment but also solidify your grasp of the topic. Ultimately, approaching your assignments methodically not only ensures academic success but also develops critical analytical skills essential for advanced studies or professional applications in mathematics.