How to Solve Problems Involving Conditional Expectation in Probability Assignments

When it comes to solving probability problems in assignments, particularly those involving conditional expectation, students often face challenges in understanding the underlying principles and applying them correctly. Conditional expectation is a crucial concept in probability theory, helping to answer questions about what to expect given certain conditions or pieces of information. This blog will break down the essential elements of conditional expectation, explain how to solve problems step-by-step, and provide tips and resources for students seeking Probability Theory Assignment Help.
If you find yourself struggling with probability assignments or need assistance with understanding how conditional expectation fits into broader concepts, seeking Math Assignment Help can offer clarity and guidance. But before seeking external support, it’s essential to develop a solid understanding of conditional expectation to tackle these problems confidently.

When it comes to solving probability problems in assignments, particularly those involving conditional expectation, students often face challenges in understanding the underlying principles and applying them correctly. Conditional expectation is a crucial concept in probability theory, helping to answer questions about what to expect given certain conditions or pieces of information. This blog will break down the essential elements of conditional expectation, explain how to solve problems step-by-step, and provide tips and resources for students seeking Probability Assignment Help.
If you find yourself struggling with probability assignments or need assistance with understanding how conditional expectation fits into broader concepts, seeking Math Assignment Help can offer clarity and guidance. But before seeking external support, it’s essential to develop a solid understanding of conditional expectation to tackle these problems confidently.
What is Conditional Expectation?
Conditional expectation refers to the expected value of a random variable, given that certain conditions or events have already occurred. In simple terms, it's the expectation of one random variable when we know something about another. This concept is often used in situations where we want to compute the average outcome of a random process under a known condition. In mathematical terms, the conditional expectation of a random variable X given an event or random variable Y is represented as E[X∣Y].
To understand this more concretely, imagine you’re rolling a die, and you know that the outcome is an even number. The conditional expectation would be the expected value of the die roll, but with the additional information that the roll resulted in an even number.
The Basics of Conditional Expectation
1. Conditional Expectation for Discrete Random Variables
For discrete random variables, the conditional expectation is calculated using the formula:
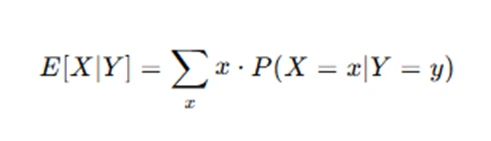
Where:
- X is the random variable whose expectation is being calculated,
- Y is the conditioning random variable,
- P(X=x∣Y=y) is the conditional probability that X=x given that Y=y.
This formula involves summing over all possible values of xxx, weighted by the conditional probabilities of X given Y.
2. Conditional Expectation for Continuous Random Variables
For continuous random variables, the conditional expectation is calculated using an integral:
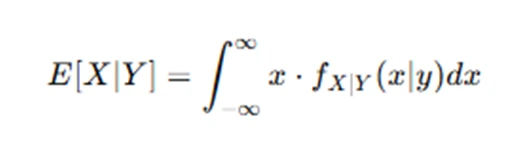
Where:
-
is the conditional probability density function of X given Y=y.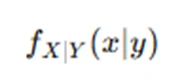
For both discrete and continuous cases, conditional expectation can be thought of as the expected value of X after taking into account the information provided by Y.
Solving Problems Involving Conditional Expectation
When tackling problems involving conditional expectation, the approach can vary depending on the specific nature of the problem. However, there are key steps and strategies that can help students systematically solve these problems.
Step 1: Understand the Problem and Identify Given Information
The first step in solving any probability problem, including those with conditional expectation, is to thoroughly read and understand the question. Carefully identify what information is given in the problem and what needs to be determined. The key to solving these problems lies in recognizing which quantities are random variables, which ones are conditioned upon, and how they are related.
For example, if you are given a joint probability distribution P(X,Y), this will allow you to compute the conditional probability P(X∣Y), which is essential for calculating the conditional expectation.
Step 2: Calculate the Conditional Probability
The next step involves determining the conditional probability P(X∣Y). This is essential because conditional expectation depends on knowing how X behaves given Y. In general, the formula for conditional probability is:
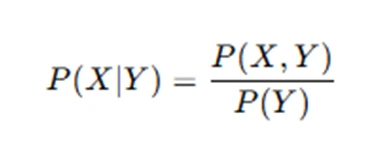
Where P(X,Y) is the joint probability of X and Y, and P(Y) is the marginal probability of Y.
In problems involving discrete random variables, you can calculate the conditional probability by using the joint probability distribution table. In the case of continuous random variables, you might need to integrate the joint probability density function.
Step 3: Apply the Conditional Expectation Formula
Once you have the conditional probability P(X∣Y), you can proceed to compute the conditional expectation using the formula for either discrete or continuous random variables, as discussed earlier.
For discrete random variables, you’ll sum the products of each possible value of X and its corresponding conditional probability. For continuous random variables, you’ll integrate over the possible values of X, multiplying by the conditional probability density function.
Step 4: Check for Additional Conditions or Assumptions
Often, probability problems come with additional conditions, such as independence or certain assumptions about the relationship between X and Y. These factors can simplify the problem and lead to more straightforward solutions.
For instance, if X and Y are independent, the conditional probability P(X∣Y) simplifies to P(X), and the conditional expectation of X given Y becomes just the expected value of X.
Step 5: Interpret the Results
Once you’ve calculated the conditional expectation, interpret the results in the context of the problem. Conditional expectation often helps to answer questions like, “What is the expected value of X given that Y takes on a specific value?”
Example Problem: Solving Conditional Expectation
Let’s go through a simple example to illustrate how to solve a conditional expectation problem.
Problem: Suppose a bag contains 5 red balls and 3 green balls. You draw two balls without replacement. Let X be the number of red balls drawn, and let Y be the total number of balls drawn. Find the conditional expectation E[X∣Y=2], i.e., the expected number of red balls drawn given that 2 balls were drawn.
Solution:
- Identify the given information: The sample space is a set of possible outcomes when drawing 2 balls. There are 5 red balls and 3 green balls, making a total of 8 balls.
- Compute the conditional probability: We need to compute P(X=x∣Y=2), the probability of drawing xxx red balls given that 2 balls are drawn. Since Y=2 means that exactly 2 balls are drawn, the possible values of X are 0, 1, and 2. We calculate the conditional probabilities for each case using combinations:
- Calculate the conditional expectation: Now that we have the conditional probabilities, we can use them to compute the conditional expectation:
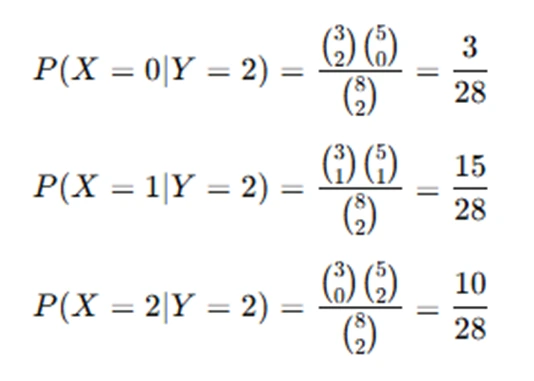
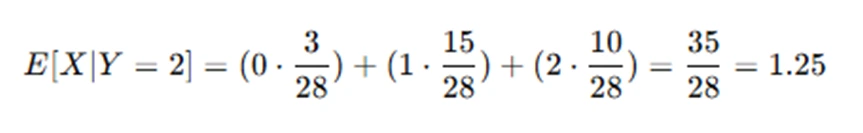
Thus, the expected number of red balls drawn given that 2 balls were drawn is 1.25.
Common Mistakes and Tips for Success
- Misunderstanding conditional probability: One of the most common mistakes in conditional expectation problems is misunderstanding how to calculate conditional probabilities.
- Overlooking independence: If two random variables are independent, this can greatly simplify the problem. In such cases, P(X∣Y)=P(X), and the conditional expectation becomes just the expected value of X.
- Forgetting to normalize probabilities: When working with discrete variables, always ensure that the conditional probabilities sum to 1. For continuous variables, verify that the probability density function integrates to 1.
- Seeking help when stuck: If you find yourself struggling with conditional expectation problems or any other part of your probability assignment, consider reaching out for Probability Assignment Help or Math Assignment Help. Sometimes, discussing the problem with an expert can provide new insights and simplify complex concepts.
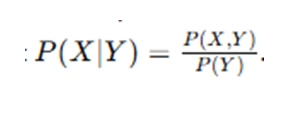
Remember that.
Conclusion
Conditional expectation is a fundamental concept in probability theory, and mastering it is essential for tackling advanced probability assignments. By following the steps outlined above and practicing with examples, you can enhance your understanding and problem-solving skills. Remember, if you're feeling stuck, don’t hesitate to seek support from tutors or experts in probability. With the right resources and a solid approach, solving conditional expectation problems can become a straightforward and rewarding process.