Understanding Finite Difference Methods for Solving Partial Differential Equations Assignments

Partial differential equations (PDEs) are fundamental to many areas of science, engineering, and mathematics. These equations describe phenomena such as heat conduction, wave propagation, and fluid dynamics, making them essential tools in modeling the natural world. However, solving PDEs analytically can be extremely challenging, particularly when the equations are complex or the boundary conditions are non-trivial. This is where computational methods, such as finite difference methods (FDM), become invaluable. This blog aims to provide a comprehensive understanding of finite difference methods and their application to solving PDEs, which is especially useful for students tackling related Differential Equations Assignments.
If you're struggling with the complexities of PDEs and need assistance, seeking Differential Equations Assignment Help can be a valuable resource. Additionally, many students also turn to Math assignment help to ensure they grasp the underlying mathematical principles and techniques. Let’s dive into the details of finite difference methods, explore how they work, and discuss their significance in the context of solving PDEs.

What Are Partial Differential Equations?
Before diving into the Finite Difference Method, it is crucial to understand what partial differential equations are and why they are important. In essence, a PDE is an equation that involves partial derivatives of a function with respect to more than one independent variable. For example, in heat transfer problems, the temperature at a given point can change over time and space, which leads to a PDE involving both time and spatial derivatives.
There are various types of PDEs, including:
- Elliptic PDEs, which describe steady-state problems (e.g., heat conduction in a material).
- Parabolic PDEs, which model time-dependent phenomena like heat diffusion.
- Hyperbolic PDEs, which describe wave propagation, such as sound or light waves.
Each type of PDE requires specific boundary conditions, which are essential for solving these equations. Depending on the problem, the boundary conditions can be fixed values, derivatives, or even more complex relations between variables.
The Need for Numerical Methods
While analytic methods can provide exact solutions to certain PDEs, many real-world problems lead to equations that cannot be solved analytically. In such cases, numerical methods like the Finite Difference Method come to the rescue, allowing for approximate solutions. These methods are particularly helpful when dealing with complicated geometries, non-linear equations, or when high accuracy is required for large-scale simulations.
In a typical Partial Differential Equations Assignment Help, students are often tasked with solving PDEs using numerical techniques. Numerical methods are advantageous because they can provide solutions that are both fast and accurate enough for practical use. Among these methods, FDM is one of the most widely taught and used in academic settings.
In a typical Partial Differential Equations Assignment Help, students are often tasked with solving PDEs using numerical techniques. Numerical methods are advantageous because they can provide solutions that are both fast and accurate enough for practical use. Among these methods, FDM is one of the most widely taught and used in academic settings.
Finite Difference Method: An Overview
The Finite Difference Method (FDM) is a numerical approach used to solve differential equations by approximating derivatives with finite differences. The core idea behind FDM is to replace the continuous derivatives in a PDE with discrete approximations, based on a grid or mesh of points in the domain. This transforms the PDE into a system of algebraic equations that can be solved using standard linear algebra techniques.
The Basic Concept of Finite Differences
In FDM, the continuous spatial domain is discretized into a grid, where the function values are approximated at each point. For example, consider a function u(x,t)u(x, t)u(x,t), which is defined in both space and time. The partial derivatives of uuu can be approximated by finite differences:
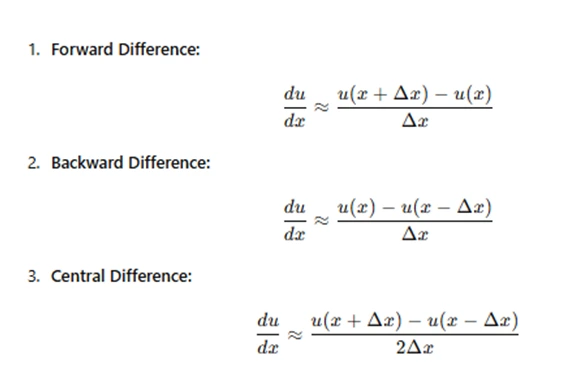
Where h is the grid spacing. For higher-order derivatives, higher-order finite difference approximations can be used.
By discretizing the entire PDE in both space and time (for time-dependent problems), we obtain a system of algebraic equations that can be solved iteratively or using direct methods.
Discretization of Partial Differential Equations
The first step in solving a PDE using FDM is to discretize both the spatial and temporal domains. For example, consider the one-dimensional heat equation, a parabolic PDE given by:
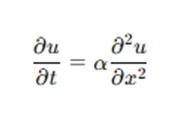
To solve this using FDM, we discretize the spatial domain into a grid of points, say x0,x1,…,xN, with spacing h, and the time domain into steps t0,t1,…,tM, with time step tΔt. The temperature at each grid point is denoted as uin, where iii represents the spatial index and n represents the time index. Using finite differences, the heat equation can be approximated as:
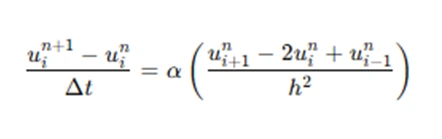
This results in a system of algebraic equations that can be solved iteratively for
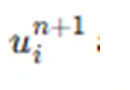
at each time step.
Types of Finite Difference Schemes
There are several types of finite difference schemes based on how the derivatives are approximated. These include:
- Explicit Scheme: In this approach, the solution at the next time step is computed directly from the known values at the current time step. This method is simple but may suffer from stability issues, requiring small time steps.
- Implicit Scheme: Here, the solution at the next time step involves solving a system of equations that incorporates the values at both the current and next time steps. Implicit methods are more stable than explicit methods, but they are computationally more expensive because they require solving a system of equations at each time step.
- Crank-Nicolson Scheme: This is a combination of explicit and implicit methods, which aims to provide a balance between stability and accuracy. It is commonly used for time-dependent problems.
Boundary and Initial Conditions
To solve a PDE using FDM, appropriate boundary and initial conditions must be specified. Boundary conditions describe the behavior of the solution at the boundaries of the domain, while initial conditions specify the state of the system at the beginning of the simulation.
For example, in the heat equation, boundary conditions could be:
- Dirichlet: The value of the solution at the boundary is fixed (e.g., the temperature at the ends of a rod).
- Neumann: The derivative of the solution at the boundary is fixed (e.g., the heat flux at the ends of a rod).
- Mixed or Robin: A combination of Dirichlet and Neumann conditions.
Initial conditions specify the temperature distribution at t=0.
Advantages and Challenges of FDM
The Finite Difference Method offers several advantages that make it a popular choice for solving PDEs:
- Simplicity: FDM is relatively easy to implement, particularly for problems with regular geometries and well-defined boundary conditions.
- Wide Applicability: FDM can be applied to a wide range of problems, including those involving heat conduction, wave propagation, fluid flow, and more.
- Flexibility: The method can be adapted to handle different types of PDEs, whether they are linear or non-linear, time-dependent or steady-state.
However, FDM also comes with certain challenges:
- Stability: In explicit methods, the time step size must be small enough to ensure stability. This may lead to long computation times for problems with small time steps.
- Accuracy: The accuracy of FDM depends on the grid resolution and the choice of finite difference approximations. Higher accuracy often requires finer grids and smaller time steps, which can increase computational costs.
- Complexity in Irregular Domains: While FDM works well for regular domains (like squares or rectangles), applying it to irregular or complex geometries requires more sophisticated techniques, such as mesh generation or adaptive grids.
When solving PDEs with FDM in assignments, students should consider several practical aspects:
- Choosing the Right Scheme: The choice between explicit, implicit, and Crank-Nicolson schemes depends on the specific problem. Explicit methods are easier to implement but less stable for stiff problems, while implicit methods are more stable but computationally intensive.
- Grid Resolution: The accuracy of the solution depends on the grid resolution. A finer grid will provide more accurate results but will also increase computational costs.
- Error Analysis: It is important to analyze the numerical error in the solution, which comes from the approximation of derivatives and the discretization of the domain. Convergence studies can help ensure that the numerical solution approximates the true solution as the grid is refined.
Conclusion
In conclusion, the Finite Difference Method is a powerful tool for solving partial differential equations numerically. Its simplicity, flexibility, and wide applicability make it an essential method in many scientific and engineering fields. Whether you're working on a Differential Equations Assignment Help or looking for Math assignment help, understanding FDM is crucial for effectively solving PDEs. By discretizing the domain and approximating derivatives, FDM transforms complex PDEs into solvable systems of equations, providing an invaluable tool for both academic and real-world problem-solving.