How to Use MATLAB for Linear Algebra Assignments

Linear algebra is one of the most fundamental topics in mathematics, and it plays a significant role in fields like computer science, engineering, physics, economics, and many others. With its wide range of applications, from solving systems of linear equations to analyzing data sets, understanding linear algebra is critical for anyone pursuing studies in these disciplines. If you’re working on linear algebra assignments, using MATLAB can help you simplify complex calculations, visualize concepts, and speed up the process. In this blog, we’ll explore how to use MATLAB effectively for linear algebra assignments and demonstrate its key features that can help you solve linear algebra assignments with ease.
MATLAB, short for "Matrix Laboratory," is a high-performance programming language and environment that is designed for numerical computation and visualization. Its powerful matrix manipulation capabilities make it an essential tool for students and professionals dealing with linear algebra. Whether you’re struggling with matrix operations, eigenvalues, or vector spaces, MATLAB can serve as your virtual assistant to solve problems more efficiently. In this post, we’ll guide you step-by-step on how to leverage MATLAB for linear algebra assignments, and offer tips for those seeking math assignment help.

Setting Up MATLAB for Linear Algebra Work
Before you dive into solving your linear algebra assignment, you first need to set up MATLAB on your computer. You can download a free trial from the official MathWorks website or use MATLAB in your institution’s computer lab if they provide access. Once you have MATLAB installed, open it and familiarize yourself with its interface. You'll find several components, such as the command window, workspace, and editor, which are essential for performing calculations and writing scripts.
To begin with, ensure that you have access to the basic functions and toolboxes related to linear algebra. MATLAB’s built-in functions make solving various matrix problems easy, so you don’t have to write complicated code from scratch. If you require additional functionalities, you can install relevant toolboxes, such as the "MATLAB Linear Algebra Toolbox."
Basic Matrix Operations in MATLAB
The core of linear algebra lies in matrices and vectors, and MATLAB is designed to handle these data structures seamlessly. The first step is to understand how to define matrices in MATLAB and perform basic matrix operations, which are foundational for solving more complex problems.
Defining Matrices
To define a matrix, simply enter the elements of the matrix inside square brackets. Separate elements of each row with spaces or commas, and separate rows with semicolons. For example:
A = [1 2 3; 4 5 6; 7 8 9]
This command creates a 3x3 matrix A. MATLAB will interpret the matrix as follows:
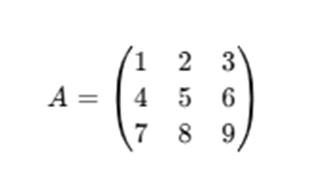
Similarly, you can define vectors in MATLAB by using either row or column format. For example:
v = [1 2 3]
This command defines a row vector with the elements 1, 2, and 3.
Matrix Operations
MATLAB provides a variety of operations for working with matrices. Some common operations include:
- Matrix addition and subtraction: Use the + and - operators to add and subtract matrices. The matrices must have the same dimensions.
- Matrix multiplication: Use the * operator to multiply matrices. Ensure that the number of columns in the first matrix matches the number of rows in the second matrix.
- Element-wise operations: To perform operations element by element (such as addition or multiplication), use the .*, .^, and ./ operators.
- Matrix transpose: Use the apostrophe (') to transpose a matrix.
A = [1 2; 3 4];
B = [5 6; 7 8];
C = A + B; % Result: [6 8; 10 12]
D = A - B; % Result: [-4 -4; -4 -4]
A = [1 2; 3 4];
B = [5 6; 7 8];
C = A * B; % Result: [19 22; 43 50]
A = [1 2; 3 4];
B = [5 6; 7 8];
C = A .* B; % Element-wise multiplication: [5 12; 21 32]
A = [1 2; 3 4];
B = A'; % Result: [1 3; 2 4]
Mastering these basic matrix operations is crucial for solving linear algebra problems efficiently in MATLAB.
Solving Systems of Linear Equations
One of the most important applications of linear algebra is solving systems of linear equations. MATLAB provides several ways to solve these systems, making it an invaluable tool for linear algebra assignments.
Using the Backslash Operator
MATLAB’s backslash operator (\) is the simplest way to solve systems of linear equations. Given a system of equations Ax=bAx = bAx=b, where A is a matrix of coefficients and b is a column vector of constants, you can find the solution vector x using:
A = [2 1; 3 4];
b = [5; 6];
x = A \ b; % Solve for x
This command will compute the values of x1x_1x1 and x2x_2x2 that satisfy the system. MATLAB uses efficient numerical methods, such as Gaussian elimination or LU decomposition, to compute the solution.
Using MATLAB’s linsolve Function
Another way to solve systems of equations is by using the linsolve function, which is more explicit than the backslash operator. It works similarly and is particularly useful when working with symbolic expressions or specific matrix types. For example:
A = [2 1; 3 4];
b = [5; 6];
x = linsolve(A, b); % Solve for x
Both methods are equally effective, but the backslash operator is more commonly used for quick solutions to linear systems.
Eigenvalues and Eigenvectors
In linear algebra, eigenvalues and eigenvectors are essential concepts. They have applications in stability analysis, optimization, and much more. MATLAB provides built-in functions to calculate eigenvalues and eigenvectors, which are crucial for solving many types of linear algebra problems.
Finding Eigenvalues and Eigenvectors
To compute the eigenvalues and eigenvectors of a square matrix A, you can use the eig function. For example:
A = [1 2; 3 4];
[eigenvalues, eigenvectors] = eig(A);
This command will return the eigenvalues in a diagonal matrix and the eigenvectors as columns in a matrix. You can extract individual eigenvalues and eigenvectors for further analysis.
Understanding the Output
The output of the eig function gives you both the eigenvalues (diagonal elements of the matrix) and the eigenvectors (columns of the eigenvector matrix). You can interpret these values to understand the matrix’s properties, such as stability or symmetry.
Advanced MATLAB Features for Linear Algebra
Beyond basic operations, MATLAB has several advanced features that can help with complex linear algebra tasks.
Singular Value Decomposition (SVD)
Singular Value Decomposition (SVD) is a powerful tool for factorizing matrices and solving linear systems, especially in applications such as data compression and signal processing. In MATLAB, you can compute the SVD of a matrix using the svd function:
A = [1 2; 3 4];
[U, S, V] = svd(A);
This function returns three matrices: U (left singular vectors), S (singular values), and V (right singular vectors). The SVD is particularly useful for dimensionality reduction in machine learning and other applications.
Matrix Inversion
Matrix inversion is often used for solving systems of linear equations, but it should be used cautiously because not all matrices have an inverse. You can compute the inverse of a matrix in MATLAB using the inv function:
A = [1 2; 3 4];
A_inv = inv(A); % Compute the inverse of A
It’s important to note that not all matrices are invertible. If the matrix is singular (i.e., it has a determinant of zero), MATLAB will return an error.
Visualizing Linear Algebra Concepts
MATLAB’s plotting functions are incredibly useful for visualizing linear algebra concepts, especially when working with vectors and matrices in two or three dimensions. For example, you can plot vectors using the quiver function:
x = [1 2];
y = [3 4];
quiver(0, 0, x(1), x(2), 0);
hold on;
quiver(0, 0, y(1), y(2), 0);
axis equal;
This code will display two vectors originating from the origin. Visualization tools in MATLAB help to better understand the geometric interpretation of linear algebra operations.
Conclusion
Even with MATLAB at your disposal, linear algebra assignments can sometimes present challenges. If you’re stuck on a particularly tricky problem, seeking math assignment help from tutors or online resources can save time and frustration. Platforms like MATLAB Central or online forums provide assistance, while professional tutors can offer one-on-one support to guide you through difficult problems.
In conclusion, MATLAB is a powerful and versatile tool for solving linear algebra assignments. From basic matrix operations to advanced techniques like eigenvalue decomposition and SVD, MATLAB offers a broad range of functions that make complex calculations more manageable. With the right approach and the help of MATLAB, you can confidently tackle your linear algebra assignments and gain a deeper understanding of the subject.