Effective Techniques for Solving Math Assignments on Composite and Homogeneous Functions

Mathematics is a subject that demands a solid grasp of theoretical concepts and the ability to apply them in practical situations. For students working on assignments related to advanced topics such as Composite and Homogeneous functions, the challenges can often seem daunting. These topics require not only understanding the fundamental definitions but also developing the skills to solve complex problems that involve combining and transforming functions. Composite functions, which involve the combination of two functions to form a new one, require a clear understanding of how inputs and outputs interact. Similarly, Homogeneous functions, which maintain a consistent form across transformations, involve recognizing patterns and understanding their applications in real-world scenarios. For students, the main hurdle is not just understanding the individual functions but mastering the way they interconnect and influence each other.
This blog is designed to simplify these advanced topics by offering clear explanations and practical examples. It focuses on breaking down difficult concepts, providing helpful tips to complete your math assignment, and offering strategies to overcome common challenges students face. By the end of this guide, students will be equipped with the knowledge and techniques needed to tackle Composite and Homogeneous functions with confidence, improving both their understanding and their ability to apply these concepts in their assignments.

What are Composite Functions?
A composite function is formed when one function is applied to the result of another function. In other words, if you have two functions, say f(x) and g(x), the composite function, denoted as f(g(x)) means that you first apply g(x) and then apply f(x) to
the output of g(x)gThis process involves combining two functions to create a new one. To evaluate a composite function, you begin by solving the innermost function and then apply the outer function to that result. Composite functions are commonly used in various mathematical and real-world scenarios where functions are dependent on each other, making them essential in fields like calculus and algebra. If we consider a function z as a function of two variables, x and y, denoted by:

Now, in this scenario, z is dependent on both x and y, and both x and y are functions of t. These relationships form a composite function of t.
Another case arises when x and y are functions of two variables u and v. In this case, we can rewrite the relationships as:
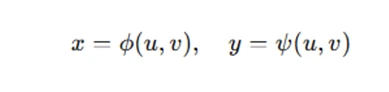
The key takeaway is that z is a composite function of u and v. It’s crucial to understand that composite functions involve multiple layers of dependency, and they are especially important when dealing with derivatives.
Studying Composite Functions for Assignments
When dealing with composite functions in assignments, it’s essential to break down the problem step by step. A common challenge students face is differentiating composite functions, especially when functions are dependent on multiple variables. For example, suppose we want to find the derivative of z with respect to t. Instead of substituting x and y back into the function and differentiating, we can use a direct formula that involves partial derivatives.
In the case of composite functions, the derivative of z with respect to t can be expressed using the chain rule, like so:
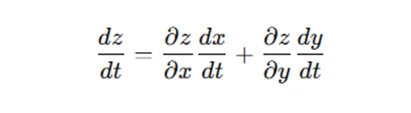
This formula simplifies the process of finding the derivative without needing to substitute the values of x and y back into the original function.
Challenges in Solving Composite Function Problems
The key challenge in solving composite function problems is understanding how different variables are interdependent. For example, x might be a function of t, and y might be a function of t as well. In such cases, z is ultimately a function of t, and we can apply the chain rule to compute the derivative.
However, these types of problems can become more complex when x and y are functions of two variables, as shown earlier. The application of partial derivatives becomes essential in differentiating functions with multiple dependencies.
Applying the Theory: An Example
Let’s consider an example where z is a function of x and y, and both x and y are functions of t:
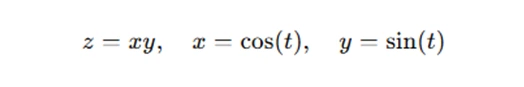
We want to find the derivative of z with respect to t. One approach would be to directly substitute x and y into the function, turning z into a function of t, and then differentiating it. However, a more efficient approach involves applying the chain rule for composite functions.
Using the formula derived earlier:
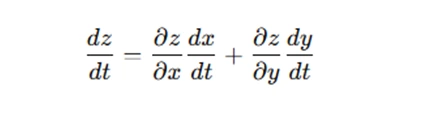
Let’s break it down:
- The partial derivative of z with respect to x is y.
- The derivative of x with respect to t is -sin(t).
- The partial derivative of z with respect to y is x.
- The derivative of y with respect to t is cos(t).

Thus, we have successfully differentiated z without needing to directly substitute x and y into the original function.
Homogeneous Functions: Theoretical Overview
Now let’s dive into homogeneous functions. A function is said to be homogeneous if it exhibits a scaling property. In other words, if the input of the function is scaled by a constant factor, the output of the function will also be scaled by some power of that constant.
For example, if we have a function f(x, y), and we scale x and y by a factor of k, we get:
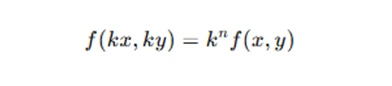
where n is a constant. The value of n determines the degree of homogeneity of the function.
Homogeneous Functions in Assignments
Homogeneous functions often arise when dealing with economics, physics, or engineering problems. In assignments, you may be tasked with finding the degree of homogeneity of a given function. This requires an understanding of Euler’s Theorem, which relates the partial derivatives of a homogeneous function to its degree of homogeneity.
Euler’s Theorem states that for a homogeneous function f(x, y) of degree n:
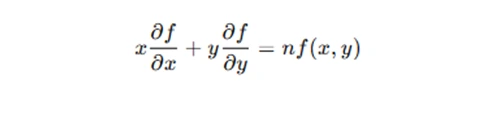
This theorem can be a powerful tool when solving problems related to homogeneous functions, especially when dealing with partial derivatives.
Challenges with Homogeneous Functions
One challenge students face when working with homogeneous functions is determining the degree of homogeneity, particularly in higher dimensions. Homogeneous functions exhibit a scaling property where multiplying all variables by a constant factor results in the function being scaled by a power of that constant. The degree of homogeneity indicates the power to which the function is scaled. In higher-dimensional functions, recognizing how each variable contributes to this scaling can become complicated, especially when the function involves multiple variables with different coefficients.
Another hurdle is the application of Euler’s Theorem, which links homogeneous functions to their partial derivatives. According to this theorem, a homogeneous function of degree n satisfies the equation where the function is equal to the sum of its partial derivatives, each multiplied by its corresponding variable. When the function involves more than two variables or contains more intricate terms, applying this theorem accurately becomes more difficult. The complexity increases as students need to compute partial derivatives and ensure they correctly interpret the contributions from each variable to the overall function. Understanding Euler’s Theorem in such contexts requires careful attention to the functional structure and its relationship to the degree of homogeneity. This can be challenging but essential for mastering more complex mathematical concepts.
Combining Composite and Homogeneous Functions
In many math assignments, you may be tasked with working on both composite and homogeneous functions, which require a deep understanding of their differentiation and application. Composite functions involve combining two or more functions into one, and to differentiate them, the chain rule is applied. This rule allows you to differentiate the outer function while treating the inner function as a constant, then multiplying by the derivative of the inner function.
On the other hand, homogeneous functions exhibit a unique property where they maintain a consistent ratio when scaled by a constant factor. Euler’s Theorem is often used to differentiate homogeneous functions, stating that the sum of the products of each variable’s partial derivative with its corresponding variable equals the degree of homogeneity.
When solving problems that involve both composite and homogeneous functions, it is crucial to combine these concepts. This allows you to handle complex relationships and multiple variables with different dependencies, making it easier to differentiate and analyze the function’s behavior in various scenarios. Mastering both techniques equips you with the tools to tackle intricate math problems efficiently.
Conclusion
In conclusion, both composite and homogeneous functions are essential concepts in mathematics that students often encounter in university-level assignments. Understanding how to study these topics, apply the theory, and tackle the challenges that arise is crucial for success. While composite functions involve multiple layers of dependency, homogeneous functions focus on scaling properties. By using tools like the chain rule and Euler’s Theorem, students can efficiently solve problems related to these topics. As you work on your assignments, remember that understanding the theoretical concepts is just as important as applying them. Practice is key to mastering these topics, and by following the strategies outlined in this blog, you can gain a deeper understanding of composite and homogeneous functions and confidently tackle your math assignments.