Efficient Methods for Solving Assignment on Numerical Analysis
Numerical Analysis is a specialized field of mathematics that deals with algorithms designed to solve your math assignment problems through numerical approximations. This area plays a critical role in solving complex problems that cannot be solved exactly, requiring practical techniques to obtain approximate solutions. If you're looking to complete your numerical analysis assignment, then it is essential to comprehend the core methods and their applications.
The main objective of these methods is to develop algorithms that can produce reliable and efficient results for problems such as solving nonlinear equations, polynomial approximations, numerical differentiation and integration, and differential equations. Understanding the practical implementation of techniques like Fixed-Point Iteration, Newton’s Method, and Lagrange Interpolation is key to approaching assignments effectively. Here’s a guide to tackling some of the core topics typically encountered in assignments, along with examples of how to approach each problem.
The Solution of Nonlinear Equations
When solving nonlinear equations, two widely used methods are Fixed-Point Iteration and Newton’s Method. Fixed-Point Iteration transforms the nonlinear equation into an iterative form where the next approximation is generated based on the previous value. This process continues until the solution converges to the desired accuracy. It is a simple and effective method, but it requires a good choice of the initial guess and convergence criteria.
Fixed-Point Iteration
In fixed-point iteration, the idea is to transform a nonlinear equation into the form x=g(x). Then, you iteratively update an initial guess until you reach convergence:
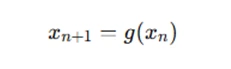
For example, to solve x2−2=0, we could rearrange the equation into the form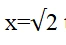 
then iterate:
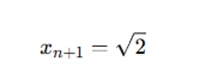
By substituting the previous value of xn into the equation repeatedly, the value of x will converge to the root.
Newton’s Method
Newton’s Method is a faster alternative, using an iterative approach to refine the guess for the root. The formula is:
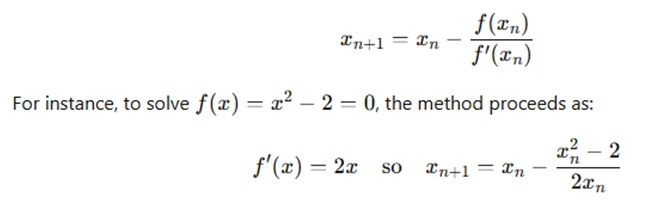
By iterating this process, you will quickly converge to the solution.
Interpolation and Polynomial Approximation
In interpolation, the goal is to find a polynomial that closely fits a set of data points, allowing you to estimate values at intermediate points. One of the most popular methods for this is Lagrange interpolation, which constructs a polynomial that passes through each of the given data points. This method uses a weighted sum of polynomials, each corresponding to a data point, and is effective for small datasets but can become computationally intensive for larger ones. Another common technique is Newton interpolation, which builds the polynomial incrementally by adding terms based on divided differences of the data points. It is more efficient than Lagrange interpolation when dealing with large datasets, as it allows for easier addition of new data points without recalculating the entire polynomial. Both methods aim to provide an accurate approximation of the underlying function that generated the data, making them invaluable tools in numerical analysis and data modeling.
Lagrange Interpolation
The Lagrange polynomial P(x) for a set of data points (x0,y0),(x1,y1),…,(xn,yn) is given by:
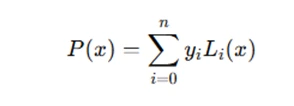
where Li(x) are the Lagrange basis polynomials:
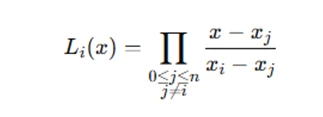
This method helps you create a polynomial that passes through each data point exactly.
Numerical Differentiation and Integration
Numerical differentiation and integration are essential techniques in computational mathematics for approximating the derivative or integral of a function when analytical methods are difficult or impossible to apply. Newton-Cotes quadrature is a family of methods that approximates integrals by interpolating the integrand with polynomials and then integrating those polynomials. It includes simple methods like the trapezoidal rule and Simpson’s rule, which are used depending on the number of points involved in the approximation. The accuracy of these methods depends on the degree of the polynomial used and the spacing between the points.
Gaussian quadrature, on the other hand, provides a more accurate method for numerical integration by evaluating the integrand at strategically chosen points, known as Gaussian nodes. These nodes are the roots of orthogonal polynomials, and the method is particularly effective for functions that are well-behaved and smooth. Both methods are widely used in numerical analysis due to their efficiency and versatility in approximating integrals and derivatives.
Newton-Cotes Quadrature
The Newton-Cotes rule provides approximations for integrals based on polynomial interpolation. For instance, the Trapezoidal Rule is a simple case of Newton-Cotes:
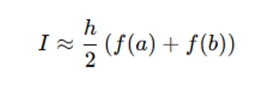
where h=b−a. This is an approximation to the integral of f(x) from a to b.
Gaussian Quadrature
Gaussian quadrature is more efficient, using weighted sums of function values at specific points. The formula for a 2-point Gaussian quadrature is:
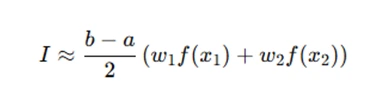
where x1,x2 are the roots of the Legendre polynomial, and w1,w2 are the corresponding weights.
Solution of Differential Equations
Ordinary Differential Equations (ODEs) are frequently encountered in numerical analysis assignments, as they are vital for modeling various real-world phenomena such as motion, growth, and decay processes. Solving ODEs typically involves approximating solutions when analytical methods are difficult or impossible to apply. To approach such problems, one-step methods like Euler's method are often employed, which compute the next value based on the current one. While simple, these methods may lack accuracy for more complex systems. To improve precision, predictor-corrector schemes are used, offering more refined approximations by first predicting the next value and then correcting it using a different estimate. Multi-step methods are also utilized for solving systems with higher accuracy over multiple intervals. Throughout these techniques, it's crucial to consider the stability and convergence of the chosen method to ensure that the solution remains reliable as the number of iterations or time steps increases. This makes ODEs a significant part of numerical analysis.
One-Step Methods for ODEs
In one-step methods like Euler’s method, the next value is computed as:
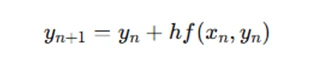
where h is the step size, and f(xn,yn) is the derivative at (xn,yn). This method provides a simple, though not always very accurate, way of approximating solutions.
Predictor-Corrector Schemes
For better accuracy, a predictor-corrector method like Heun’s method is used. It predicts the next value and then corrects it using an average of the predicted and actual derivatives:
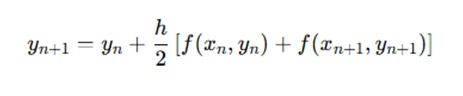
Multi-Step Methods and Stability
For more complex problems, multi-step methods like Adams-Bashforth can be used. Stability and error analysis are crucial here; ensuring that the method converges and remains accurate as the number of steps increases is essential for reliable solutions.
Conclusion
When working on Numerical Analysis assignments, it's crucial to grasp the core principles of each method. These techniques are designed to approximate solutions to complex mathematical problems that may not have exact solutions. Understanding the theory behind methods such as Fixed-Point Iteration, Newton’s Method, or Newton-Cotes Quadrature ensures you're not just applying formulas, but also recognizing when and why to use them. For example, Fixed-Point Iteration requires transforming a nonlinear equation into a format suitable for iterative solving, while Newton's Method refines guesses with faster convergence. Similarly, methods like Lagrange Interpolation and Gaussian Quadrature allow for efficient polynomial fitting and integration of functions, respectively. For differential equations, one-step methods like Euler’s method provide basic approximations, while more advanced schemes such as Predictor-Corrector methods improve accuracy. Each method involves careful iteration and error analysis, which are essential for reliable results. Mastering these techniques enables effective problem-solving in a range of complex numerical scenarios.