How to Prove the Implicit and Inverse Function Theorems in Assignments for Best Grades

Alton Caprio

Australia

Multivariable Calculus

Alton Caprio, a seasoned mathematics educator with a degree in Applied Mathematics from UC Berkeley University, has over 10 years of experience teaching multivariable calculus. With a passion for helping students excel, Alton provides expert guidance on complex topics like the Implicit and Inverse Function Theorems.

Hire Me To Do Your Multivariable Calculus Assignment

The Implicit Function Theorem: Introduction and Statement

The Implicit Function Theorem (IFT) is a powerful tool that allows us to solve systems of equations implicitly. It is especially useful when you cannot explicitly solve for one variable in terms of others. In simple terms, the theorem helps us deduce that a function exists implicitly, even when it is not easy to express it explicitly.

Statement of the Implicit Function Theorem

The Implicit Function Theorem states that if you have a system of equations with a function F(x,y)=, and you wish to solve for y as a function of x (denoted as y=f(x)), there are conditions under which this is possible. Specifically, if F(x,y) is a continuously differentiable function in some neighborhood around a point (a,b), and if (∂F/∂y)≠0 at (a,b) then there exists a function y=f(x) such that F(x,f(x))= 0.

This can be interpreted as: if the system can be differentiated with respect to y, and the derivative is non-zero, then y can indeed be solved as an implicit function of x.

Step-by-Step Proof of the Implicit Function Theorem

Step 1: Set up the function

Let’s begin by considering a function F(x,y) where F is continuously differentiable with respect to both variables. Suppose that at a point (a,b), the equation F(a,b)=0 holds true, and that ∂F/∂y≠0 at this point. We aim to show that there exists a function y=f(x) near x=a such that F(x,f(x))=0.

Step 2: Applying the Implicit Function Theorem

To prove the existence of such a function f(x), we use the method of local linear approximation (the idea behind the derivative approximation). We assume that y can be written as a function of x near a, say y=f(x). We seek to show that this function satisfies the equation F(x,f(x))=0 near a.

Step 3: Constructing the approximation

By the multivariable chain rule, we can differentiate F(x,f(x)) with respect to x to obtain:

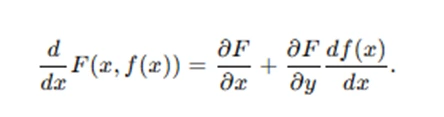
At x=a, since F(a,b)=0, we want the derivative to be zero. Rearranging gives the derivative of f(x):

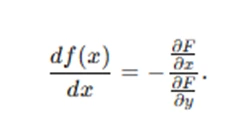
Step 4: Conclude existence and continuity

By applying the continuity of F(x,y) and its partial derivatives, we can conclude that the function f(x) exists in a neighborhood around a, and f(x) is continuously differentiable.

The Implicit Function Theorem can be tricky, but once you break it down into manageable parts—establishing the function, applying the chain rule, and ensuring the conditions of the theorem are met—you can easily tackle this proof in an assignment setting.

The Inverse Function Theorem: Introduction and Statement

The Inverse Function Theorem deals with the concept of invertibility of functions, particularly when the function is a mapping between Euclidean spaces. It provides conditions under which a function has a locally invertible map and tells us how to find its inverse function. It is an essential tool in multivariable calculus and analysis.

Statement of the Inverse Function Theorem

The Inverse Function Theorem states that if 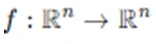is a continuously differentiable function, and the Jacobian matrix of f, denoted as Df(a), is invertible at some point a, then there exists a neighborhood around a where f is a diffeomorphism. This means that f has a continuously differentiable inverse function in that neighborhood.

Step-by-Step Proof of the Inverse Function Theorem

Step 1: Consider the function f

Let 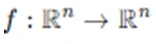be a continuously differentiable function, and let Df(a) denote the Jacobian matrix of f at a. Assume that Df(a) is invertible. Our goal is to prove that there exists a neighborhood of a where f is invertible, and that the inverse of f is continuously differentiable.

Step 2: The Jacobian matrix and its inverse

The key to proving this theorem is to consider the linear approximation of the function f around the point a. If Df(a) is invertible, then for small changes in x near a, the function f behaves like a linear map. This allows us to apply the mean value theorem for vector-valued functions.

Step 3: Construct the inverse function

Since Df(a) is invertible, there exists a matrix M=(Df(a))−1 such that for small enough perturbations, we can find an inverse function g(x) that maps points in a neighborhood of f(a) back to the corresponding points in a neighborhood of a.

Step 4: Showing the continuity and differentiability of the inverse

By using the fact that Df(a) is invertible and that the function f is continuously differentiable, we can show that the inverse function g is also continuously differentiable in a neighborhood of a. This is done by verifying that the conditions for the inverse function to be continuously differentiable are met by examining the differentiability of the mapping.

Conclusion of the Proof

We have shown that if Df(a) is invertible, then there exists a neighborhood of a where the function f is invertible, and its inverse is continuously differentiable.

Tips for Tackling These Theorems in Your Assignment

To prove the Implicit and Inverse Function Theorems effectively in your assignments, here are some useful tips:

1. Understand the Conditions Carefully

Both theorems have specific conditions that must be met, such as the non-zero derivative in the Implicit Function Theorem and the invertibility of the Jacobian in the Inverse Function Theorem. Carefully verify that these conditions are satisfied before proceeding with the proof.

2. Use the Chain Rule and Linear Approximation

The chain rule and linear approximation play a crucial role in both proofs. Make sure you understand how to apply these tools to break down complex expressions and simplify the problem.

3. Work Through Examples

Before attempting the proofs in your assignment, work through simple examples to get a sense of how the theorems work. This will help you build intuition for the steps involved.

4. Write Clearly and Methodically

When writing your proofs, be clear and methodical. Make sure to define all terms and explain each step logically. A well-written proof can demonstrate not only that you understand the material but also that you can communicate your understanding effectively.

Conclusion

Proving the Implicit Function Theorem and the Inverse Function Theorem in your multivariable calculus assignments can be challenging, but with a clear understanding of the conditions and applying the right techniques, you can excel in these proofs. Remember to break down each proof into logical steps, use tools like the chain rule and linear approximation, and verify the conditions carefully. By mastering these theorems, you’ll not only improve your understanding of calculus but also boost your chances of securing the best grades in your assignments.

By following these strategies, you can confidently tackle these theorems and succeed in your multivariable calculus assignment. Whether you're working through the Implicit Function Theorem or the Inverse Function Theorem, with the right approach, you're sure to perform well and gain a deeper understanding of the mathematical concepts at play.