How to Approach and Solve Linear Programming Assignments

Linear programming is a powerful mathematical technique for optimizing a given objective function subject to constraints. To effectively solve your linear programming assignment problems in this domain, a structured and topic-specific approach is essential. This article delves into the key areas of linear programming and provides detailed explanations for tackling these topics.
Linear Inequalities and Related Concepts
Linear inequalities form the foundation of linear programming problems. Techniques such as Fourier-Motzkin elimination can simplify systems of inequalities to a manageable form. Begin by isolating variables in a step-by-step manner:
- Identify the variable to eliminate and write the inequality in terms of it.
- Combine inequalities to reduce dimensions iteratively.
- Verify feasibility by ensuring all inequalities remain consistent.

The theorems of the alternative, such as Farkas' Lemma, can help determine whether a system of inequalities has a solution or not. Understanding polyhedral geometry, which explores the shapes formed by feasible regions, aids in visualizing solutions. For example, consider the system of inequalities:
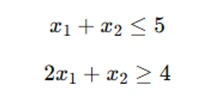
To eliminate x2x_2x2, we first rewrite the inequalities:
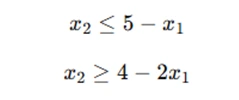
Now, combining the inequalities, we get the condition:
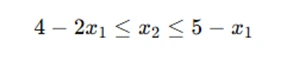
Thus, we have reduced the system to a simpler form.
Theorems of the Alternative provide conditions that allow you to determine whether a system of linear inequalities has a solution. These theorems are crucial in optimization problems, as they help prove the existence or non-existence of solutions without solving the entire system.
Polyhedral Geometry helps visualize the feasible region as a polyhedron, and these inequalities define the faces of this polyhedron.
Simplex Methods
Linear programming problems often involve exploring the optimal solution within a feasible region, and simplex methods play a pivotal role in efficiently navigating this process. These techniques ensure a systematic approach to improving the objective function while maintaining feasibility, making them essential for solving real-world optimization problems.
Primal Simplex Method
The primal simplex method involves moving along the edges of a polyhedron to reach the optimal vertex. Start by:
- Converting the problem into standard form (inequalities to equalities).
- Identifying a feasible starting solution (often using artificial variables).
- Iteratively pivoting using entering and leaving variables to improve the objective value.
Suppose we have the following linear programming problem:
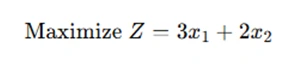
subject to:
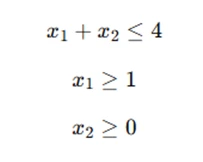
The Simplex method would begin with an initial basic feasible solution and iterate through the corners of the feasible region defined by these constraints to find the optimal values of x1 and x2 that maximize Z.
Dual Simplex Method
This method works when the primal is infeasible but the dual is feasible. It follows a similar pivoting process but focuses on maintaining dual feasibility while achieving primal feasibility.
Parametric Primal-Dual Method
This approach gradually changes the coefficients of the objective function or constraints, solving a series of related linear programs. It’s useful for problems where parameters vary dynamically.
Sensitivity Analysis
Sensitivity Analysis in linear programming helps determine how sensitive the optimal solution is to changes in the problem’s parameters. It is particularly useful for understanding how variations in the objective function’s coefficients or the right-hand side values of constraints affect the optimal solution.
The analysis involves finding the range of values over which the current optimal solution remains unchanged. If the parameter is adjusted beyond this range, the optimal solution might change. This is crucial in decision-making contexts where certain factors may vary, such as in supply chain management or financial optimization. For instance, consider the objective function:
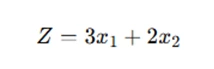
and the constraint:
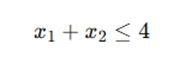
If the coefficient of x1x_1x1 changes to 4, we need to examine how this change affects the optimal values of x1x_1x1 and x2x_2x2. Sensitivity analysis provides the range within which this change can occur without altering the optimal solution.
Degeneracy and Cycling
Degeneracy occurs when a linear programming problem has multiple optimal solutions, or the Simplex method revisits the same basic feasible solution without progressing toward the optimal solution. This can lead to cycling, where the algorithm continuously loops through the same solutions without improving.To resolve cycling, techniques such as Bland’s Rule are applied, which ensures that the algorithm follows a path toward the optimal solution by selecting the entering and leaving variables in a systematic and non-repetitive order. This avoids revisiting the same solution and ensures convergence.
Revised Simplex Method
The Revised Simplex Method is a more computationally efficient version of the Simplex method. Instead of maintaining the entire simplex tableau (which can be large and cumbersome), this method only keeps track of the necessary components of the tableau (such as the inverse of the basis matrix and the current objective function values).
By doing this, the Revised Simplex method reduces memory usage and computational effort, making it faster, especially for large-scale problems. It also tends to be more stable in terms of numerical precision when dealing with floating-point operations.
Duality and Complementary Slackness
Duality is a central concept in linear programming, where every linear programming problem (the primal problem) has an associated dual problem. The dual problem provides another perspective on the same optimization problem and is often easier to solve or analyze. The dual variables in the dual problem represent the shadow prices or marginal values of the constraints in the primal problem.
Complementary Slackness refers to the relationship between the primal and dual solutions. Specifically, for each constraint, either the primal variable corresponding to that constraint is at its bound (active) or the dual variable is zero. This helps identify which constraints are "binding" (i.e., determining the optimal solution) and which are not.
Dantzig-Wolfe Decomposition
The Dantzig-Wolfe Decomposition is used to decompose large-scale linear programming problems into smaller subproblems that are easier to solve. This method is particularly useful for problems that can be broken down into independent subproblems, such as in integer programming.
The decomposition reduces the original problem to a master problem and several subproblems. The master problem coordinates the subproblems, and column generation is used to iteratively add variables (columns) to improve the solution.
Knapsack Problem
The Knapsack Problem is a classic optimization problem where you are given a set of items, each with a weight and a value, and the goal is to maximize the total value without exceeding a given weight limit.
This problem is typically solved using dynamic programming, which breaks the problem into smaller subproblems, and the integer programming approach is often used to ensure that the solution consists of whole items (i.e., no fractions).
Column Generation
Column Generation is a method used to solve large integer programming problems where it’s not feasible to include all variables upfront. Instead, you solve a restricted version of the problem by considering a subset of variables (columns) and iteratively adding new columns that improve the objective function.
This method is widely used in the cutting stock problem, which involves minimizing the number of cuts needed to produce a set of desired items from raw materials. The problem is typically solved using column generation, where you solve a restricted master problem and generate new columns (cuts) based on the solution of the subproblem.
Total Unimodularity
A matrix is totally unimodular if every square submatrix has a determinant of 0, +1, or -1. This property is significant because it guarantees that a linear programming problem with integer constraints will have an integer solution.
This property can be used to simplify the solution of integer programming problems by leveraging linear programming techniques instead of resorting to more complex integer programming methods.
Network Flows and the Network Simplex Method
Network flows problems are optimization problems where the objective is to optimize the flow of materials, goods, or information through a network, subject to capacity constraints on the edges. These types of problems are often modeled as a directed graph, where nodes represent locations, and edges represent the paths between them.
The Network Simplex Method is a variation of the Simplex method used specifically for solving network flow problems. It operates on the structure of the network, focusing on edges and nodes rather than variables and constraints, making it more efficient for network-related LP problems.
Subgradient Optimization
Subgradient optimization is used for solving optimization problems where the objective function is not differentiable (i.e., it does not have a well-defined gradient). This method generalizes gradient descent by using subgradients instead of gradients. A subgradient is a vector that provides a "generalized" direction of descent at a non-differentiable point.
Subgradient optimization is commonly used for convex optimization problems, such as minimizing non-smooth convex functions.
Ellipsoid Method
The Ellipsoid Method is a specialized algorithm used to solve convex optimization problems. It iteratively refines the feasible region by inscribing an ellipsoid inside the current feasible region and then updating it in each iteration. The method is notable for its ability to solve large-scale convex problems, even when the feasible region is highly complex.
Although not as commonly used as other methods like Simplex or Interior-Point, the Ellipsoid method has strong theoretical guarantees and is particularly effective for certain types of problems, such as those with a large number of constraints and variables.
Conclusion
Linear programming assignments involve key concepts like optimization, constraints, and objective functions. Understanding these concepts theoretically is important, as it helps you solve your math assignment problems related to linear programming systematically. Having a strong foundation in linear programming enables you to apply various methods to find optimal solutions for real-world problems. If you ever need help with math assignments, there are many resources available to guide you through these challenging topics. These resources offer expert support and provide a structured approach to learning, making it easier to grasp complex concepts and improve your problem-solving skills.