How to Tackle Questions on Indeterminate Forms using L'Hôpital's Rule

In mathematics, particularly in calculus, indeterminate forms refer to expressions that yield undefined or ambiguous results when directly substituted into an equation. Common examples include 0/0, ∞/∞, 0 × ∞, ∞ - ∞, 0^0, and ∞^0. These forms can appear when evaluating limits, making them difficult to solve using basic methods. The primary challenge is that these expressions don't provide an immediate, clear value, leading to confusion.
To handle indeterminate forms, one of the most effective techniques is L'Hôpital's Rule. This rule applies when you encounter forms like 0/0 or ∞/∞. It states that if a limit produces an indeterminate form, you can differentiate both the numerator and the denominator and then re-evaluate the limit. This process simplifies the expression, allowing you to resolve the ambiguity and find a definite value.
Understanding how to recognize and apply L'Hôpital's Rule is crucial for solving calculus problems involving indeterminate forms. In assignments and exams, mastering this technique can help you approach complex limits with confidence. Practicing these methods regularly will ensure you become proficient in handling indeterminate forms efficiently and accurately.

What Are Indeterminate Forms?
Indeterminate forms arise when the limit of a ratio or expression leads to an ambiguous value that cannot be immediately determined. Common indeterminate forms include:
- 0/0: The expression appears to be 0 divided by 0.
- ∞/∞: This expression suggests infinity divided by infinity, which is also undefined.
- 0 × ∞: An indeterminate form where 0 is multiplied by infinity.
- ∞ - ∞: The subtraction of two infinite values.
- 0^0: Zero raised to the power of zero.
- ∞^0: Infinity raised to the power of zero.
For example, when solving for limits, expressions like sin (x−1)/x−1 and x2−1/ x−1 are indeterminate forms because, when you substitute x=1, you end up with 0/0 for both. Similarly, the expression 1−cos(x)/x becomes 0/0 when x=0.
These forms do not have an immediate, obvious value, and thus require special techniques to resolve.
Handle Indeterminate Forms in Assignments
When tackling assignments that involve indeterminate forms, it's crucial to know how to handle these tricky expressions. Rather than attempting a direct substitution, one must often manipulate the expression or use advanced techniques to evaluate the limit.
One of the most effective tools for resolving indeterminate forms is L'Hôpital's Rule, a fundamental principle of calculus that simplifies the evaluation of limits. But before we dive into that, let's take a closer look at the theoretical background and how you might encounter these forms in assignments.
The Generalized Mean Value Theorem (Cauchy’s Mean Value Theorem)
A vital concept that frequently comes up when working with indeterminate forms is the generalized mean value theorem (also known as the Cauchy Mean Value Theorem). This theorem plays a significant role in understanding how indeterminate forms behave, and it provides the foundation for applying L'Hôpital's Rule.
The Cauchy Mean Value Theorem states that if two functions, f(x) and g(x) are continuous on a closed interval [a, b] and differentiable on the open interval (a, b), and if the derivative of g(x), denoted g′(x), does not vanish anywhere inside the interval, then there exists a point ccc within (a, b) where the following relationship holds:
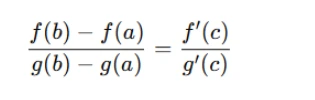
This relationship will be crucial when we explore how to apply L'Hôpital's Rule to indeterminate forms. Essentially, the theorem helps us understand how the behavior of the derivative at a particular point can help resolve indeterminate forms in the context of limits.
L'Hôpital’s Rule: A Key Tool for Handling Indeterminate Forms
One of the most powerful tools for resolving indeterminate forms is L'Hôpital's Rule. This rule applies to situations where both the numerator and denominator of a fraction approach zero or infinity as xxx approaches a certain value.
The rule states that for functions f(x) and g(x) that are differentiable in an open interval (a, b), if the following conditions hold:
- Both f(a)=0and g(a)=0, or both f(x)→∞ and g(x)→∞ as x→a
- The derivatives f′(x) and g′(x) exist in the interval (a, b), and g′(x)≠0.
Then, the limit of the ratio f(x)g(x) as x approaches a can be computed as:
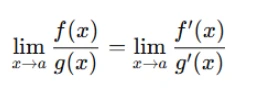
In other words, if you encounter a 0/0 or ∞/∞ form when calculating a limit, you can apply L'Hôpital’s Rule by differentiating the numerator and denominator and then re-evaluating the limit.
Step-by-Step Process for Using L'Hôpital’s Rule
When you first encounter an indeterminate form like 0/0 or ∞/∞, it can be tricky to know how to move forward. But don’t worry, L'Hôpital’s Rule is here to help! Let’s break it down into a clear process and discuss how to use it effectively.
Step 1: Check the Indeterminate Form
The very first thing you need to do is make sure that the expression you’re working with actually results in an indeterminate form. For instance, if you’re trying to find the limit of f(x)g(x) as x→ax \to ax→a, and direct substitution gives you something like 0/0 or ∞/∞, you’re in the right place to apply L'Hôpital’s Rule. These forms are tricky because they don’t give us a clear answer right away. So, confirming that you have one of these forms is crucial.
Step 2: Differentiate the Numerator and Denominator
Once you’ve confirmed that you’ve got an indeterminate form, it’s time to apply L'Hôpital’s Rule. What you do next is differentiate both the numerator and the denominator of the fraction separately. This step is the core of the rule. You’re essentially swapping the original expression for a new one, where you’re looking at the rates of change of both parts of the fraction.
For example, if you have the expression sin(x−1) and you’re looking to find the limit as x→1, you’ll first differentiate the numerator, which is sin(x−1), and the denominator, which is just x - 1.
Step 3: Re-evaluate the Limit
After differentiating both the numerator and the denominator, it’s time to re-evaluate the limit. This is where you take a step back and look at the new expression you created after applying the derivatives. If the new expression no longer gives you an indeterminate form, then you’re done. Just calculate the limit as usual.
For example, after differentiating, if the expression cos(x−1) results in a non-indeterminate form when you plug in x=1, you’ve successfully resolved the limit. This often happens when L'Hôpital’s Rule simplifies the expression enough for you to directly calculate the limit.
Step 4: Repeat the Process if Necessary
Sometimes, even after applying L'Hôpital’s Rule, you may end up with another indeterminate form. If that happens, don’t worry! You can simply apply L'Hôpital’s Rule again. Differentiate the numerator and denominator once more and try re-evaluating the limit. This iterative process can help break down more complex indeterminate forms.
For instance, if your new differentiated expression still gives you something like 0/0, you can apply the rule again, and with each step, the expression should gradually simplify until you reach a clear answer.
Step 5: Conclude the Limit
Once you’ve applied the rule enough times and you no longer get an indeterminate form, you’ll be able to directly compute the limit. That’s the beauty of L'Hôpital’s Rule—it’s an efficient way to resolve difficult limits by converting an indeterminate form into something manageable.
Examples to Illustrate L'Hôpital’s Rule
Let’s go through a couple of examples to understand how to apply L'Hôpital’s Rule in practice:
Example 1: Resolving sin (x−1)/x−1 as x→1
At first glance, this seems like a 0/0 form when you substitute x=1 into the expression. However, applying L'Hôpital’s Rule can help.
- Differentiate the numerator: d/dx sin(x−1)=cos(x−1).
- Differentiate the denominator: d/dx(x−1)=1.
Now, take the limit:
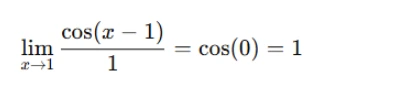
Thus, the value of the limit is 1.
Example 2: Resolving x2−1/x−1 as x→1
At first, substituting x=1gives 0/0, but after simplifying and applying L'Hôpital’s Rule, we get:
- Differentiate the numerator: d/dx(x2−1)=2x.
- Differentiate the denominator: d/dx(x−1)=1.
Now, take the limit:
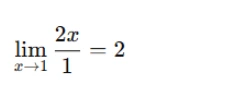
Thus, the value of the limit is 2.
Common Challenges When Using L'Hôpital’s Rule
While L'Hôpital’s Rule is an invaluable tool, there are a few challenges that students may encounter:
- Repeated Indeterminate Forms: Sometimes, applying L'Hôpital’s Rule results in another indeterminate form (such as 0/0 or ∞/∞). In these cases, you can apply the rule multiple times until the indeterminate form resolves.
- Non-differentiable Functions: If the functions involved are not differentiable at the point of interest, L'Hôpital’s Rule cannot be applied. In these cases, you may need to look for alternative methods, such as simplifying the expression or using other limit properties.
- Understanding the Context: In some problems, L'Hôpital’s Rule may not be the best method to resolve an indeterminate form. It is essential to understand when to apply it and when to use other techniques, like factoring or expanding series.
Conclusion
Indeterminate forms are a challenging yet fundamental part of calculus, especially when solving limits. Understanding how to approach and resolve these forms is essential for university students, particularly when working on math assignments. By applying L'Hôpital's Rule and following a systematic approach, students can effectively solve their math assignment and handle these problems with confidence.
Remember, the key to mastering indeterminate forms and L'Hôpital’s Rule is practice. The more you practice solving these types of problems, the more proficient you'll become at recognizing and handling them in your assignments and exams. Keep working on examples, use L'Hôpital’s Rule effectively, and soon you'll be able to solve even the most complex indeterminate forms in your math assignments with ease.