Effective Techniques for Solving Differential Equations Assignments

Differential equations are foundational in understanding many physical, biological, and engineering systems. Whether you're tackling parabolic, hyperbolic, or elliptic equations, each type requires a specialized approach for accurate solutions. Assignments involving differential equations often test your understanding of both theoretical concepts and practical methods used to solve these equations.
Solving differential equations assignment, it's crucial to grasp the underlying principles behind the various types of equations. For parabolic equations, methods like the ?-method and maximum principle play a key role in ensuring the stability and convergence of the solution. Hyperbolic equations often require an understanding of the CFL condition and Fourier analysis to manage wave propagation and numerical stability. Elliptic equations, on the other hand, demand expertise in boundary conditions, error analysis, and methods like the finite element method for numerical solutions.

Incorporating these techniques into your assignments will not only help you arrive at the correct solutions but also enhance your ability to think critically about the problem-solving process. Whether you're solving for steady-state temperature distributions, wave propagation, or electrostatic potential, mastering these methods will allow you to effectively tackle and complete your differential equations assignment with confidence and precision.
Parabolic Equations: Unraveling Heat Transfer and More
Parabolic equations are often encountered in heat conduction problems, such as heat distribution over time. The classical equation for a parabolic problem is the heat equation:
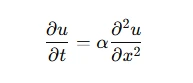
Where u(x,t) represents temperature at position x and time t, and α is the thermal diffusivity constant. The solution to such an equation is heavily influenced by the chosen method for solving it.
One key method is the ?−method, which involves discretizing time and space to approximate solutions in numerical form. This method ensures that the solution converges as the step sizes in both dimensions shrink, ultimately leading to more accurate solutions.
For heat transfer problems, the maximum principle states that the maximum value of the solution is found on the boundary of the domain. This property helps in ensuring that solutions are well-behaved and bounded. Convergence of a numerical scheme means that as the time and spatial step sizes tend to zero, the solution should converge to the exact solution.
The Locally One-Dimensional (LOD) method is often applied when the problem is almost one-dimensional. In such cases, the spatial derivatives in higher dimensions are treated as if they only vary in one direction, simplifying the problem and making it more computationally efficient.
Hyperbolic Equations: Understanding Wave Propagation
Hyperbolic equations arise when solving problems related to wave propagation, such as sound waves or fluid dynamics. The general form of a hyperbolic equation can be written as:
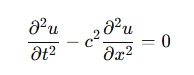
Where ccc is the wave speed. For solving such equations numerically, two key concepts are often discussed: the CFL condition and Fourier analysis.
The CFL condition (Courant–Friedrichs–Lewy condition) sets a stability limit on the time step relative to the spatial step size for solving hyperbolic equations. It ensures that information does not propagate faster than the computational grid can resolve, which helps prevent numerical instabilities.
Fourier analysis helps in solving hyperbolic problems by decomposing the solution into a series of sinusoidal functions. This approach is especially useful when the solution has periodic or oscillatory behavior, which is often the case in wave problems.
Numerical schemes for hyperbolic equations typically involve solving conservation laws. For example, the method of Godunov’s scheme can be employed to maintain the conservation property of the solution, ensuring that physical quantities like mass or energy are conserved over time.
Elliptic Equations: Solving Steady-State Problems
Elliptic equations, such as Laplace’s equation, are commonly encountered when modeling steady-state phenomena like electrostatic potential:
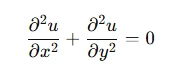
For these equations, the error analysis involves examining how errors propagate through the solution process. The maximum principle also applies, ensuring that the maximum or minimum values of the solution occur on the boundary of the domain.
Boundary conditions are crucial when solving elliptic equations. The most common types are Dirichlet and Neumann conditions. Dirichlet boundary conditions specify the values of the function at the boundary, while Neumann conditions specify the values of the derivative of the function at the boundary.
A powerful technique for solving elliptic equations numerically is the variational formulation. This method converts the differential equation into an optimization problem where the goal is to find the function that minimizes a certain energy functional. The finite element method (FEM) is widely used for this purpose, discretizing the domain into small elements and solving the problem piece by piece.
Properties of Numerical Schemes: Consistency, Convergence, and Stability
When solving differential equations numerically, it is essential to ensure that the numerical scheme employed is consistent, meaning the difference equations approximate the continuous differential equations as the step sizes approach zero. Convergence ensures that as the step sizes become smaller, the numerical solution approaches the exact solution, while stability guarantees that errors do not grow uncontrollably over time.
The finite difference method is one of the most common numerical techniques used to solve differential equations. It involves approximating derivatives by finite differences and then solving the resulting system of algebraic equations
For a given differential equation, such as:
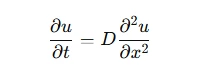
The finite difference approximation is given by:
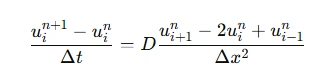
Where uin represents the numerical approximation of u(xi,tn) at grid points xi and time steps tn.
Conclusion
In conclusion, solving differential equations involves a blend of analytical techniques and numerical methods. Whether working with parabolic, hyperbolic, or elliptic equations, understanding the underlying principles is crucial for selecting the right approach. By applying methods like the ?-method for parabolic equations, the CFL condition for hyperbolic equations, or the finite element method for elliptic equations, you can systematically break down complex problems and derive accurate solutions. It's important to also consider the properties of numerical schemes, such as consistency, convergence, and stability, to ensure the reliability of the results. As you continue to tackle these assignments, remember that mastering these techniques will not only help with your math assignment but will also deepen your understanding of the mathematical modeling of real-world phenomena. Embrace these methods to approach each problem methodically and solve your math assignments with confidence and precision.